Googleの話題になった看板を今さらながら素人がグダグダに解いてみた(笑)
10年以上も前なので、今さらって話なのだけれど、ご存知ない方の為にいちおう説明すると、上の看板は、2004年にシリコンバレーの101号線沿いに建てられた奇妙な看板だ。意味不明な看板なので、最初は相手にされなかったみたいだけれど、やがて、これがGoogleの求人広告である事が分かり、話題になったやつだ。(^^;
看板には
{first 10-digit prime found in consecutive digits of e}.com
と書かれている。日本語にすると、
{eの連続する桁で、最初に出てくる10桁の素数}.com
となる。これを解くと、7427466391.com となり、ここへアクセスすると、またクイズのような問題があり、それを解いて、次のページに進むと、ようやくGoogleの求人情報が出てくるといったものだったようだ。
この、{eの連続する桁で、最初に出てくる10桁の素数}ってのを解いて、7427466391.comって答えに僕も辿り着いてみたいと、昨晩、ふと思い、やってみたのだ。(笑)
「eの連続する桁」ってのは、理科系の人には馴染みの深い自然対数の底eのことだ。これは、円周率みたいにどこまでも続く数字だ。e=2.718・・・・・
ここで、ふと、eの定義って、なんだったけかと思ったが、特に興味もないので、そこはとばして、eの数列が何万桁も掲載されいるページがあるので、こちらでその数列の一部を適当に拝借。
e=
2.71828182845904523536028747135266249775724709369995957496696762772407663035354759457138217852516642742746639193200305
99218174135966290435729003342952605956307381323286279434907
63233829880753195251019011573834187930702154089149934884167
50924476146066808226480016847741185374234544243710753907774
49920695517027618386062613313845830007520449338265602976067
37113200709328709127443747047230696977209310141692836819025
51510865746377211125238978442505695369677078544996996794686
44549059879316368892300987931277361782154249992295763514822
08269895193668033182528869398496465105820939239829488793320
36250944311730123819706841614039701983767932068328237646480
つまり、この永遠に続く数字を左から10桁、2718281828、7182818284、1828182845と、一つずつ、ずらしていった時に最初に出てくる素数を求めろって問題だ。
ここで、素数ってのは、皆さんご存知の通り、1と自分自身以外には約数を持たない自然数の事だ。つまり、上の1番最初に出てくる数字2718281828であれば、1から順番に2718281828まで、割ってみて、割り切れる数字がなければ、素数って事になる。でも、それだと、1つの数字に対して10億回以上の割り算をしなければならず、死んでしまう。そこで、素数かどうか判定するために、出来る限り計算回数を減らすロジックを考えることになる。そのロジックはあちらこちらのサイトに出ているので、ここでは書かないけれど、調べると、そんなロジックを利用した素数判定のエクセルのユーザー定義関数を作っている方がいらっしゃるので、最初は、それを使おうと思ったんだけど、やってみると、大きい数字では、どれもエラーになってしまい、使い物にならない事が判明。
ここで、素数かどうか判定する一つのロジックに、調べたい数字の平方根以下の素数で割って、割り切れなければ素数って事になるってのがある。このロジックもあちこちに説明があるので省略するけど、上の場合、10桁なので、10の10乗の平方根、10の5乗つまり10万以下の素数で、割り切れるか見てやればいいことになる。
そして、これも、こちらのページに素数の一覧があるので、そこから10万以下の素数を拝借。拝借したものを見ると、10万以下の素数は9592個なので、これで、随分と割り算の回数は減ることになる。とは言っても、えらい数だけど・・・。(笑)
ということで、ここからが本題で、これを表計算ソフトを使って計算させるのだ。
エクセルのVBAが詳しい人なら、ロジック的には簡単に処理する為のVBAマクロなり関数を組めそうな気がするが、少なくとも、上に書いたように、色んな人の素数判定のユーザー定義関数を試したが、大きな数字だとエラーになっちゃうし、自分でもVBAをいじってみたが、うまくいかないので、超ベタに、縦軸に9592個の素数、横軸にとりあえず200個ほど、eの数列を左から1つずつずらしたものを入れた超巨大な表を作って計算させる事にしてみたのだ。(笑)
これなら、普通のエクセルの使い方だけで十分で、やる事は簡単だと思ったんだけど、数が増えると、ところがどっこいってのが、出てきたので、それを書いてみたかったのだ。(笑)
まず、表の縦軸の9592個の素数は、上の素数が書かれたテキストファイルをダウンロードして、エクセルで開いて、縦方向の配置を選択すればよいので、問題はない。横軸は、数字を一つずつずらすので、関数を使う。
まず、Sheet2のA1セルに、上のeの数列の小数点をとったものを貼付けておき、この表でいうと、C1セルに、次のような関数を入れる。
=MID(Sheet2!$A$1,COLUMN()-2,10)
MIDは指定された文字列の指定した位置から、指定した数だけ文字を抽出する関数だ。
上の式で言うと、「Sheet2!$A$1」がSheet2に貼り付けたeの数列だ。あとでオートフィルで式をコピーする関係上A1セルは絶対参照にしてある。COLUMN()ていう関数は、列番号を返す関数で、表のC1セルは3列目なので、3が返ってくる。マイナス2がついてるので、C1セルでは1ということになる。今回は、とりあえず200番目までやってみるので、横軸に200、この表だとGT1セルまで、オートフィルでひっぱって式をコピーすれば、左から一つずつずらした数字の横軸は完成だ。
ちなみに、後でふれるけれど、200もひっぱるのが、めんどくさければ、マクロで処理すれば良いこになる。
次は横軸を縦軸の素数で割る計算式の入力だ。
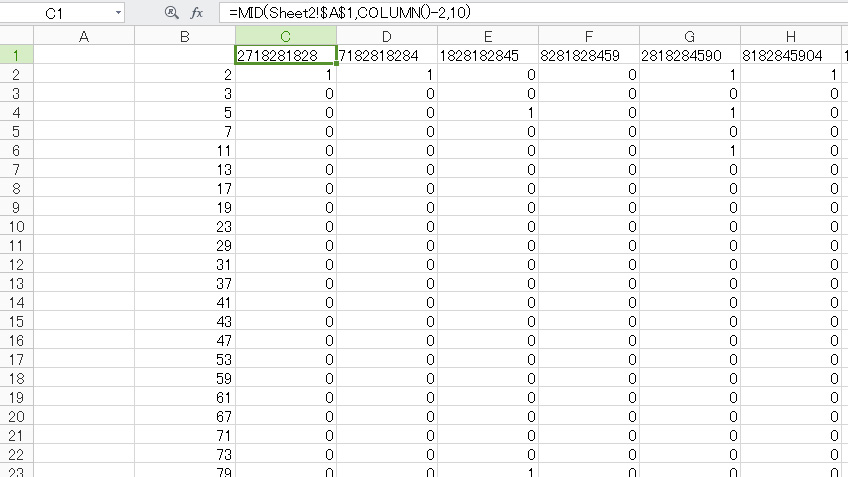
=IF(MOD($C$1,B2)=0,1,0)
入力されている関数の意味だけど、IF関数は、有る条件に対して、真ならA、偽ならBって感じに値を返す関数で、MODは割り算の余りを返す関数だ。だから上の式の意味はC1をB2で割った余りが0、つまり、余りがなければ1を、余りがあれば0を入力するって意味だ。ここで、あとで、縦軸の素数9592個分、下にオートフィルでコピーする事を考えると、常に割られるセルはC1でなければならないので、C1は絶対参照で、$C$1でなければならない。
ところが、この絶対参照が問題で、逆に横軸にオートフィルでコピーする場合は、割られるセルが可変で、割るセルが固定でなければならないので、以下のようでなければならない。
=IF(MOD(C1,$B$2)=0,1,0)
列数が10や20なら、横軸パターンの式をオートフィルでひっぱってから、縦軸方向にオートフィルでひっぱるために、相対参照と絶対参照を書き直していけばいいけれど、200もあると、それだけでも、大作業になってしまう。
そこで、探してみると、こちらのページにすべてのセル参照を絶対参照にするというマクロがあったので、このマクロを使わせてもらう事にした。
まず横軸用の式をオートフィルで200番目まで入力したあと、上記のマクロを実行すると、式は以下のようになる。
=IF(MOD($C$1,$B$2)=0,1,0)
この状態で、$B$2を単純にB2に置換してやれば、縦軸のオートフィル用の式の200列全てが出来上がる。
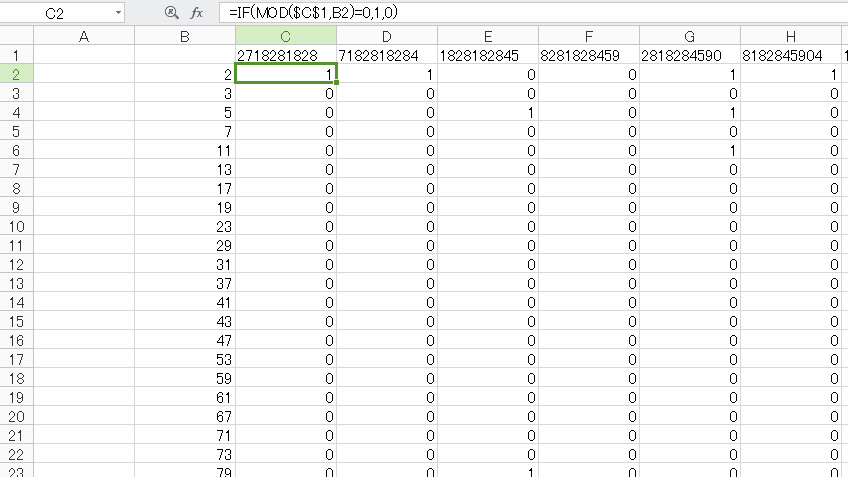
そしたら、いよいよ、この横軸に入った式を一気に行ごと9593行目まで、オートフィルでコピーするわけだけど、数が数なので、手でひっぱると死んでしまうので、最初、数行だけひっぱる操作を「マクロの記録」で記録する。記録したものをVBEでひらいて、行を9593に変更。
書き直したこのマクロを実行してやれば、一気に9593行目までのオートフィルが完成だ。
そして、いよいよ最後は、素数かどうかの判定の式だけど、これは、簡単なのだ。(^^)
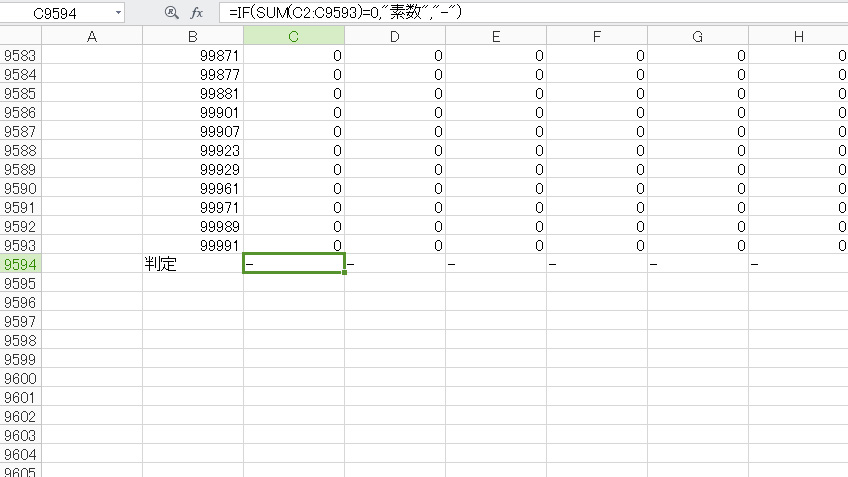
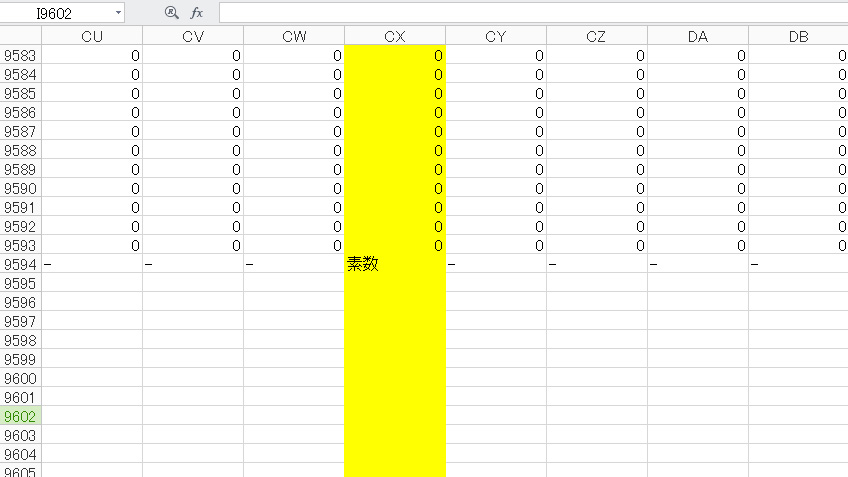
=IF(SUM(C2:C9593)=0,”素数”,”-“)
表の個々の計算の返り値は、割り切れたら1、割り切れなかったら0だから、列の全ての計算結果が0なら、素数ってことになる。ということで、式の意味は、列の合計が0なら「素数」を返し、0でなければ「-」を返すってだけの単純なものだ。これを、横軸にオートフィルで引っ張って、完成なのだ。(^^)
結果としては、100番目に答えである最初の素数7427466391が出てくる。
ちなみに、200番目までには、
100番目:7427466391
124番目:7413596629
150番目:6059563073
172番目:3490763233
183番目:2988075319
と、5つの素数が出現するのだ。
2.718281828459045235360287471352662497
75724709369995957496696762772407663035
35475945713821785251664274274663919320
030599218174135966290435729003342952
60595630738132328627943490763233829880753195251019・・・・・
そして、当然のごとく思うのが、看板が
{first 10-digit prime found in consecutive degits of π}.com
と、eではなく円周率のπだったら、どうなんだろうと思うわけで、eのかわりにπの数列を入れてみると、なんの事はない、いきなり5番目に最初の10桁の素数5926535897が出てきちゃって、チャンチャンって感じでごぜーました。(^^;
以上、Googleの看板をプログラミングを一切使わずに、エクセルでベタベタで解いてみたって話でした・・・。(^^;
追記です。
めでたく7427466391.comにアクセスできると、
Congratulations. You’ve made it to level 2. Go to www.Linux.org and enter Bobsyouruncle as the login and the answer to this equation as the password.
f(1)= 7182818284
f(2)= 8182845904
f(3)= 8747135266
f(4)= 7427466391
f(5)= __________
ってのが表示されたそうです。
www.Linux.orgに行き、BobsyouruncleをID、f(5)の値をパスワードにして、ログインしろって事ですね。
これはクイズみたいなもので、f(1)からf(4)が自然対数の底eの中の数列であるって事と、それぞれの数字の和が49って事に気づけば、解くのは簡単です。こういうのは僕はセンスが無いので、たぶん、和が49ってのは、当時見ても、なかなか気づかなかったんじゃないかって気がしますけど・・・。(笑)
解き方は今回使った表の横軸をそのまま使います。
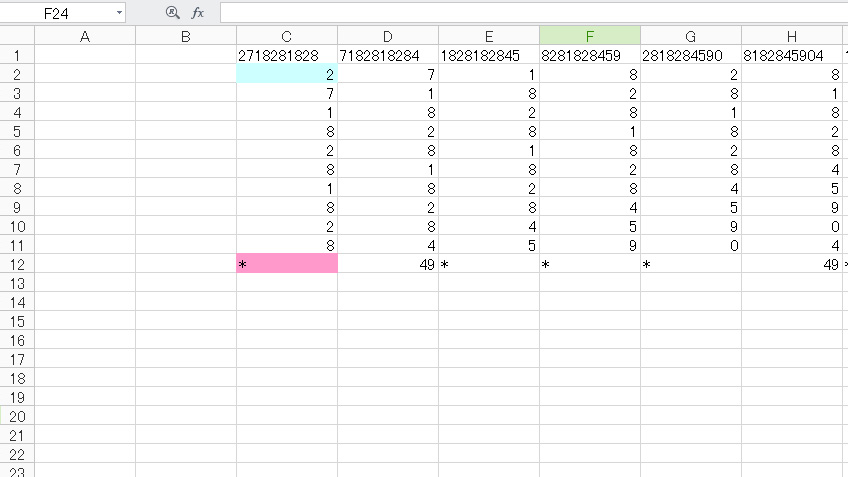
水色のセル
=VALUE(MID($C$1,ROW()-1,1))
関数はC1セルの左から1番目の数字を1つ取り出すって意味です。MIDは上で使いましたよね。ROW()は行番号の取得です。VALUEは文字列として取り出したものを数値に変換する関数です。
ピンクのセル
=IF(SUM(C2:C11)=49,49,”*”)
これは、上でやったのと全く一緒ですけど、列の和が49だったら、49を返し、そうでなかったら*を返すってことですね。
関数のオートフィルの要領は、最初の看板のところでやったやり方と同じです。
表が完成したら、横にスクロールして49になっているところを見ていくと、答えは130番目に出てくる「5966290435」というのが分かります。
これで、はれてwww.Linux.orgにログインすると、初めて求人の募集要項が見れたって事のようです。(^^;
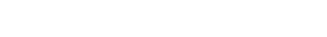








どうでもいいですが
lim[t->0](1+t)^(1/t)をeとして定義しています
eの定義を補足して頂き、ありがとうございます。(^^)
数学を勉強したのが、かれこれ30年前なので、お恥ずかしながら、もう、ほとんど覚えていません。
こんなふうに補足していただけるのは、有難い限りです。(^^(